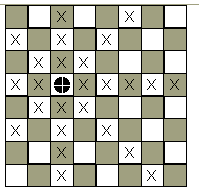
The eight Queens problem is another puzzle than can be solved by means of recursive backtracking. For those of you unfamiliar with the game of chess, it is played on an 8 x 8 grid of squares. Various pieces can be placed on this board, with no more than one piece on a given square. The Queen is the most powerful piece in the game, in that it can travel vertically, horizontally, and diagonally any number of squares on a single turn, provided it does not have to pass through another piece. For example, in the grid at right, the Queen can move to any of the marked squares.

A queen is said to threaten another piece it can move to the same square as that piece on a single turn. Thus, the above Queen would threaten any piece in a marked square. The object of the Eight Queens problem is to place eight Queens on a chessboard in such a way that no Queen threatens any other Queen.

You want to place eight Queens on the board, and so it would make sense that each step would consist of placing another Queen in a legal position. Determining where to search for a legal move, however is a little tricky. Rather than viewing the board as consisting of 64 squares. it can be seen as being comprised of eight columns, each with eight rows. Because Queens can move any number of squares vertically in a single turn, and because you are placing eight Queens on the board, there must be exactly one queen in every column. Thus, rather than having to place eight Queens in 64 squares, you instead want to place one Queen in each of the eight columns.

The recursive case, therefore, consists of picking a safe row in the given column, placing a Queen there and then making a recursive call to find a solution given that placement. If a solution is found, then you're done. Otherwise, pick another safe row, and repeat.

Now, what about the base case? Since each recursive call moves you into another column, and there are only eight columns, you hit one base case when you step into column nine. You don't actually use column nine, but remember how your recursion works.

When else does the recursive case break down? It places a Queen in a safe row and make a recursive call. If that call fails to find a solution, it picks another safe row and make another recursive call. This continues until all the safe rows have been tried. At that point you know that the path you are on is a dead end, and so the procedure ends unsuccessfully.