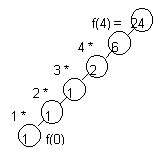To Recurse or Not to Recurse

Analysis
Data Structures & Program Design by Robert L. Kruse, Chapter 7, contains a good discussion of Recursion as does C++ fo You ++ by Litvin & Litvin, Chapter 19

Iteration vs. Recursion
One device in deciding whether to write a module recursively is the recursion tree. Let us examine two modules used earlier. For the call factorial(4), observe the tree:
	
int factorial (int n)
{
	if ( n == 0 )
		return 1;
	return  n * factorial ( n - 1);
}

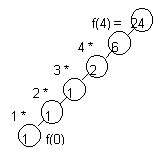When the tree is linear, the module can be written as easily iteratively. 

int factorial ( int n )
}
	int fact = 1;
	for ( int index = 1;  index <= n;  index++)
		fact = fact * index;
	return fact;
}

Another Example:
int fibo ( int n)
{
	if ( n < 3)
		return 1;
	else
		return  fibo (n - 1) + fibo ( n - 2);
}

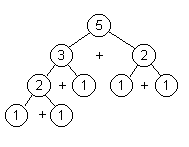For the call fibo(5) observe the tree. Even with two calls to the function, there is much redundancy. Written iteratively:
int fibo (int n )
{	if ( n < 3 )
		return 1;
	else
	{	int f;
		int a = 1;
		int b = 1;
		for ( int index = 3;  index <= n;  index++)
		{	f = a + b;
			a = b;
			b = f;
		}
		return f;
	}
}
Tail Recursion
If space is a consideration then tail recursion should probably be removed. Tail recursion is a recursive call at the end of the module. In a recursive module, memory locations are held until the module is completed, thus occupying more space than if the variables were changed directly. The previous example of removal of tail recursion is from the Robert L. Kruse book on Data Structures & Program Design.

To Recurse or not to Recurse
Since recursion can always be replaced by iteration and, perhaps, use of a stack and conversely, we need to question our use of recursion.

  1. If a program involves stacks, would recursion be more natural and understandable?
  2. Is the recursive code clearer?
  3. If a recursion tree results in a chain then iteration is probably as straightforward.
  4. If a recursion tree results in duplications then recursion is probably inefficient.
  5. Tail recursion should be avoided if space is a consideration.
The Litvins in their text C++ for You ++ state that "recursion should be used when it significantly simplifies the code without excessive performance loss." They suggest that recursion is very useful for dealing with Recursion should be avoided in linear structures (factorial) or linear processes (sequential search). Iteration is easier and more efficient in these situations involving tail recursion.

Continue to:  Unit 3 / Prev / Next