This problem goes back to Leonardo de Pisa, better known as Fibonacci, who posed the following interesting problem in 1202.

If we start with one pair of newborn rabbits of opposite sex, then how many pairs of rabbits are there at the end of one month, two months, three months, four months, . . and so on, if we assume the following:

• It takes a newborn rabbit two months to mature into an adult rabbit;
• a pair of adult rabbits of opposite sex produces one pair of newborn rabbits also of opposite sex each month; and
• the rabbits never die.

End of First Month	End of Second Month	End of Third Month

1. What happens at the end of the fourth month? the fifth month? etc.
2. We express this sequence:

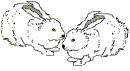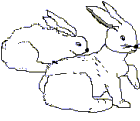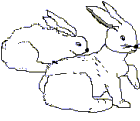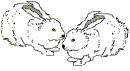   n	1	2	3	4	5	6	7	. . .	n
   f(n)	1	1	2	3	5	8	13

   f(x)		1	when x < 2
   		f(x - 1) + f(x - 2)	when x * 2

   Evaluate f(10)

   Write a function for the above.

The Towers of Hanoi
"In the great Temple of Hanoi there is a large brass slab on which there are three diamond needles each a cubit high, and as thick as the body of a bee. At the beginning of the world, God places 64 gold disks with holes in their centers on one of these needles, the largest resting on the brass slab, and the others decreasing in size to the top. Day and night, the priests transfer the disks from needle to needle, one disk at a time, one each second, and only moved so that disks are placed on either a free needle, or on a larger disk."

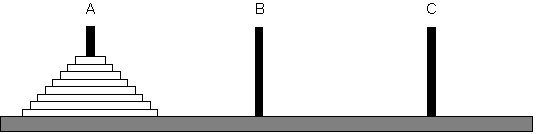
As the legend goes, when all 64 disks are on another needle, the temple will crumble, and the world will come to an end. How long will it take the priests to move all the disks?

Can you write an expression for finding when the world will end?

What if there were n disks?

Write the function recursively. In general, k disks can be transferred from needle A to needle by carrying out the following steps.

1. Transfer the top (k - 1) disks from needle A to needle B recursively
2. Transfer the remaining disk on needle A to needle C
3. Transfer the (k-1) disks on needle B to needle C recursively

Exercises

1. What value does Answer(5) return?
   A. 8
   B. 10
   C. 16
   D. 32
   E. 120

      int answer ( int n )
   {
      if ( n == 1 )
         return 2;
      return 2 * answer( n - 1);
   }

2. If n is a positive integer, how many times will Answer be called to evaluate Answer (n) (including the initial call)?
   A. 2
   B. n
   C. 2n
   D. n2
   E. 2n